你知道这些求极限的方法吗?
你知道这些求极限的方法吗?
当然,求极限是数学中一个非常重要的概念,特别是在微积分、实分析等领域。这里,我将为你介绍几种常用的求极限的方法,这些方法既适用于函数极限,也部分适用于数列极限。

一、代数法
这是最直接也是最基础的方法。当极限表达式可以通过代数运算简化时,我们可以先对表达式进行因式分解、合并同类项、约分等操作,然后再求极限。
二、直接代入法
如果极限表达式中的自变量趋近于某个确定值时,函数值有明确的结果,那么可以直接代入该值来求极限。但需要注意的是,直接代入法可能不适用于某些未定式的极限,如0/0型或∞/∞型。
三、洛必达法则
洛必达法则是求解0/0型或∞/∞型未定式极限的一种重要方法。其基本思想是,当极限形式为0/0或∞/∞时,可以对分子和分母分别求导,然后求导后函数的极限。需要注意的是,洛必达法则的使用需要满足一定的条件,如分子分母在极限点附近都可导,且分母导数不为零。
四、等价无穷小代换
当极限表达式中存在可以等价替换的无穷小时,我们可以利用等价无穷小代换简化表达式,从而更容易地求出极限。常用的等价无穷小有sinx~x,tanx~x,e^x-1~x等。
五、夹逼定理(或沙漏定理)
夹逼定理适用于求解一些难以直接计算的极限。基本思想是通过找到两个函数来夹住目标函数,使得这两个函数的极限相等并且都趋近于目标函数的极限,从而可以推断出目标函数的极限。
六、泰勒公式展开法
泰勒公式展开法是将函数在某一点处展开成幂级数,然后利用级数的性质来求解极限。这种方法在处理复杂函数或复合函数的极限时非常有效。
七、单调有界准则
单调有界准则主要用于求解数列的极限。如果一个数列单调递增(或递减)且有上界(或下界),那么这个数列的极限存在。通过证明数列的单调性和有界性,我们可以确定数列的极限。
八、定积分定义法
对于某些特定形式的数列极限或函数极限,我们可以将其转化为定积分的形式来求解。这种方法在处理与求和或积分相关的极限问题时非常有用。
以上这些方法各有特点,适用于不同类型的极限问题。在实际应用中,我们需要根据具体问题的特点选择合适的方法。同时,还需要注意各种方法的适用范围和限制条件,以确保求解过程的正确性和结果的准确性。
-

- 南京周杰伦演唱会盛况再现:千山万水,热血沸腾
-
2025-09-22 13:47:30
-

- 缅甸果敢冲突:政治战下的生存之战!
-
2025-09-22 13:45:14
-

- 老山前线二等功臣——张荣
-
2025-09-18 14:47:13
-

- 海贼:库赞
-
2025-09-18 14:44:58
-

- 陈赫英雄联盟玩的6 手速辣眼 堪比肖奈
-
2025-09-18 14:42:42
-

- 2023世界500强企业榜单完整版
-
2025-09-18 14:40:26
-

- 2018湖南卫视华人春晚节目单官方版 嘉宾明星阵容名单
-
2025-09-18 14:38:11
-

- 9张手绘漫画,看到泪目……
-
2025-09-18 14:35:55
-

- 《爱情路上风雨多》这才是真正原唱,唱出爱的真谛,好听百...
-
2025-09-18 14:33:40
-
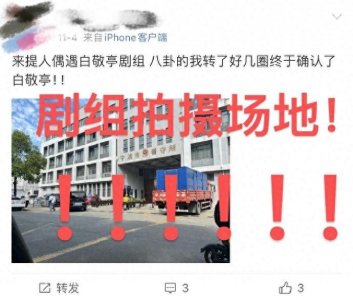
- “白敬亭在宁波嫖娼被抓”?刚刚警方回应!
-
2025-09-18 14:31:24
-

- 转给爱旅游的TA!137个国家森林城市大全
-
2025-09-18 14:29:09
-
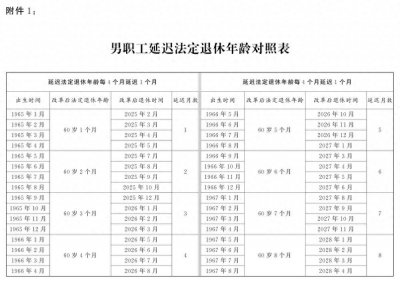
- 延迟法定退休年龄时间对照表公布
-
2025-09-18 14:26:53
-

- 全球犹太人居住人数最多的国家是以色列
-
2025-09-17 16:48:42
-

- "灌篮高手"系列壁纸 这次是流川枫专场哦,最后三张是电脑壁纸~
-
2025-09-17 16:46:26
-

- 潮流壁纸|"死神"系列 帅气的黑崎一护,上次留言要死神的快收图~
-
2025-09-17 16:44:10
-
- Brown Eyed Girls成员Narsha公开比基尼照 完美比例引热议
-
2025-09-17 16:41:55
-
- 「每天学点英语单词」shoulder
-
2025-09-17 16:39:39
-

- 《辛德瑞拉和四名骑士》主演确定 大发阵容引期待
-
2025-09-17 16:37:24
-
- “大旋涡套小旋涡”海陵岛又见龙卷风
-
2025-09-17 16:35:08
-
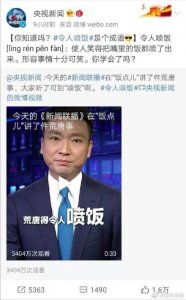
- 央视科普,“令人喷饭”是个成语
-
2025-09-17 16:32:52


 难得的好小品演员,黄杨 在饭米粒儿中饰演黄小黄
难得的好小品演员,黄杨 在饭米粒儿中饰演黄小黄 唐朝刺史是几品?唐朝刺史相当于现在什么官
唐朝刺史是几品?唐朝刺史相当于现在什么官 otc是什么意思(OTC是什么意思?深入解析OTC市场)
otc是什么意思(OTC是什么意思?深入解析OTC市场) 略备薄酒还是略备薄宴 略备薄酒以小酌的意思
略备薄酒还是略备薄宴 略备薄酒以小酌的意思 玉化砗磲手串一般多少钱?这份价格清单请收好
玉化砗磲手串一般多少钱?这份价格清单请收好 张云雷为什么是回族 张云雷的回族名字叫什么
张云雷为什么是回族 张云雷的回族名字叫什么 ky是什么梗?ky到底是什么意思?
ky是什么梗?ky到底是什么意思? galgame鉴赏:十二魔器之一 重口猎奇作《解体插入新书》
galgame鉴赏:十二魔器之一 重口猎奇作《解体插入新书》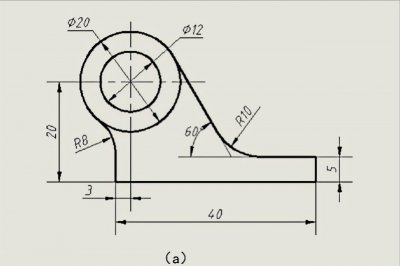 机械制图基础知识:圆弧、圆弧连接及其正确画法
机械制图基础知识:圆弧、圆弧连接及其正确画法 曾梦想仗剑走天涯是什么歌谁唱的 曾经的你完整歌词介绍
曾梦想仗剑走天涯是什么歌谁唱的 曾经的你完整歌词介绍